فرمول هایی برای تولید عدد پی

عدد گنگ پی یکی از اعداد ویژه ریاضی است که قرن ها ریاضی دانان را به خود مشغول نموده است. این عدد که حاصل تقسیم محیط یک دایره بر طول قطر آن می باشد عددی متعالی است به عبارت دیگر قابل ترسیم نیست. عدد پی تا ۱۰۰ رقم اعشار به صورت زیر است:

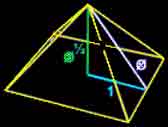
بررسي یک حالت ازحالت هاي ممكن رابطه فیثاغورس 

آیا میدانستید که دارکوب ها قادرند ۲۰ بار در ثانیه به تنه درخت ضربه بزنند ؟

آیا میدانستید که یک خرس قادر است با سرعت یک اسب بدود ؟

آیا میدانستید که موریانه ها قادرند تا ۲ روز زیر آب زنده بمانند ؟

آیا میدانستید که اختاپوس سه قلب دارد ؟

آیا میدانستید که مورچه ها هرگز نمی خوابند ؟

آیا میدانستید که حلزون ها می توانند تا سه سال بخوابند و در این مدت هیچ غذایی نخورند ؟

.......... بقیه را در ادامه ی مطلب بخوانید

بی خبر از همدگر آسوده خوابیدن چه سود

                            بر مزار مردگان خویش نالیدن چه سود

زنده را باید به فریادش رسید

                            ورنه بر سنگ مزارش آب پاشیدن چه سود

زنده را تا زنده است قدرش بدان

                           ورنه بر سنگ مزارش کوزه گل چیدن چه سود

زنده را در زندگی دستش بگیر

                           ورنه مشکی از برای مرده پوشیدن چه سود

.....

اطلاعات زير در شمارش اعداد بالاتر ازميليارد به کار می رود:

1000000000000   (تريليون). trillion  
1000000000000000   (كوآدريليون).quadrillion
1000000000000000000   (كوئين تيليون).quintillion
1000000000000000000000   (سكستيليون).sextillion
 1000000000000000000000000   (سپتيليون).septillion
1000000000000000000000000000   (كوئين تيليون).quintillion
1000000000000000000000000000000  ( نوريليون).norillion
10000000000000000000000000000000000000000000000000  (كوئيندسيليون).quindecillion.

خـداونـد از نـگاه ملاصـدرا


خداوند بی نهایت است و لا مکان و بی زمان
اما بقدر فهم تو کوچک میشود
و بقدر نیاز تو فرود می آید
و بقدر آرزوی تو گسترده میشود
و بقدر ایمان تو کارگشا میشود
و به قدر نخ پیر زنان دوزنده باریک میشود
و به قدر دل امیدواران گرم میشود

یتیمان را پدر می شود و مادر
بی برادران را برادر می شود
بی همسرماندگان را همسر میشود
عقیمان را فرزند میشود
ناامیدان را امید می شود
گمگشتگان را راه میشود
در تاریکی ماندگان را نور میشود
رزمندگان را شمشیر می شود
پیران را عصا می شود
و محتاجان به عشق را عشق می شود

خداوند همه چیز می شود همه کس را
به شرط اعتقاد
به شرط پاکی دل
به شرط طهارت روح
به شرط پرهیز از معامله با ابلیس
 

بشویید قلب هایتان را از هر احساس ناروا
و مغز هایتان را از هر اندیشه خلاف
و زبان هایتان را از هر گفتار ِناپاک
و دست هایتان را از هر آلودگی در بازار

و بپرهیزید
از ناجوانمردیهــا
ناراستی ها
نامردمی ها!

چنین کنید تا ببینید که خداوند
چگونه بر سر سفره ی شما
با کاسه یی خوراک و تکه ای نان می نشیند
و بر بند تاب، با کودکانتان تاب میخورد
و در دکان شما کفه های ترازویتان را میزان میکند
و در کوچه های خلوت شب با شما آواز میخواند

مگر از زندگی چه میخواهید
که در خدایی خدا یافت نمیشود؟
که به شیطان پناه میبرید؟
که در عشق یافت نمیشود
که به نفرت پناه میبرید؟
که در حقیقت یافت نمیشود
که به دروغ پناه میبرید؟
که در سلامت یافت نمیشود
که به خلاف پناه میبرید؟
و مگر حکمت زیستن را از یاد برده اید
که انسانیت را پاس نمی دارید ؟!

رابطه ای برای ضرب

تعداد رقم ها

کسر مسلسل

کسرهای مصری

آیا میدانستید که خورشید روزانه معادل صد و بیست و شش هزار میلیارد اسب بخار انرژی به زمین می‌فرستد ؟

آیا میدانستید که زمین از حیث بزرگی پنجمین و از حیث فاصله با خورشید، سومین سیاره منظومه شمسی است ؟

آیا میدانستید که هر ساله حدود پانصد شهاب‌سنگ نسبتا" بزرگ به زمین برخورد می‌کند ؟

آیا میدانستید که ایرانیان اولین بار نمایش های همگانی (تئاتر) را اجرا نموده اند و همانها گریم و ساخت نقاب را در ۱۵ هزار سال پیش پایه گذارده اند ؟

آیا میدانستید که گرده گل هرگز فاسد نمی شود و از محدود مواد طبیعی است که تا زمان نامحدودی باقی می ماند ؟

آیا میدانستید که لاکپشت در بین جانوران جهان، طولانی ترین عمر را دارد و ممکن است تا۱۵۰سال عمر کند ؟

آیا میدانستید که بیشتر سردردهای معمولی از کم نوشیدن آب میباشد ؟

آیا میدانستید که نمک از پنج هزار سال پیش در سفره ما انسانها بوده است ؟

آیا میدانستید که خرگوش و طوطی تنها حیواناتی هستند که می‌توانند بدون برگشتن اشیاء پشت سر خود را ببینند ؟

..........

 تاريخچه عدد صفر

اولين نکته شايان ذکر در مورد عدد صفر اين است که اين عدد دو کاربرد دارد که هر دو بسيار مهم تلقي مي شود يکي از کاربردهاي عدد صفر اين است که به عنوان نشانه اي براي جاي خالي در دستگاه اعداد (جدول ارزش مکاني اعداد) بکار مي رود. بنابراين در عددي مانند 2106 عدد صفر استفاده شده تا جايگاه اعداد در جدول مشخص شود که بطور قطع اين عدد با عدد 216 کاملاً متفاوت است. دومين کاربرد صفر اين است که خودش به عنوان عدد بکار مي رود که ما به شکل عدد صفر از آن استفاده مي کنيم.

هيچکدام از اين کاربردها تاريخچه پيدايش واضحي ندارند. در دوره اوليه تاريخ کاربرد اعداد بيشتر بطور واقعي بوده تا عصر حاضر که اعداد مفهوم انتزاعي دارند. بطور مثال مردم دوران باستان اعداد را براي شمارش تعداد اسبان، ... بکار مي برند و در اينگونه مسائل هيچگاه به مسئله اي برخورد نمي کردند که جواب آن صفر يا اعداد منفي باشد.......

مهندسان هخامنشی راز استفاده از عدد پی (۱۴/۳ = π) را 2500 سال پیش کشف کرده بودند. آن ها در ساخت سازه های سنگی و ستون های مجموعه تخت جمشید که دارای اشکال مخروطی است، از این عدد استفاده می کردند.
عدد پی( ۳.۱۴ = π) در علم ریاضیات از مجموعه اعداد طبیعی محسوب می شود. این عدد از تقسیم محیط دایره بر قطر آن به دست می آید. کشف عدد پی جزو مهمترین کشفیات در ریاضیات است. کارشناسان ریاضی هنوز نتوانسته اند زمان مشخصی برای شروع استفاده از این عدد پیش بینی کنند. عده ی زیادی، مصریان و برخی دیگر، یونانیان باستان را کاشفان این عدد می دانستند اما بررسی های جدید نشان می دهد هخامنشیان هم با این عدد آشنا بودند........

قضیه چهار رنگ به صورت ساده این است: یک نقشه داریم میخواهیم ثابت کنیم می توان کشورها را با ۴ رنگ، رنگ کرد به صورتی که هر دو کشور مجاور ناهمرنگ باشند.

این مسئله برخلاف ظاهر ساده اش سال ها فکر دانشمندان را به خود مشغول داشت تا در حدود ۱۹۷۶ کی اپپل وهیکن. بعد از این که ۲۵ سال از عمرشان را وقف اثبات این نظریه کردند، توانستند ثابت کنند که اگر برای حدود ۱۰۰۰۰ نقشه (گراف) ای که لیست شده بودند این کار امکان پذیر باشد آنگاه برای همه ی نقشه ها این کار ممکن است. این تعداد نقشه با کمک کامپیوتر و برنامه ای که آن ها نوشته بودند ، طی روزها تلاش و در طول ۱۲۰۰ ساعت فعالیت سریعترین کامپیوتر زمان خود حل شد. آن ها در واقع در ابتدا قصد استفاده از کامپیوتر را نداشتند ولی ناچار به این کار شدند. بعد کسانی پیدا شدند و گفتند این که نشد اثبات و این دو نفر کلی تلاش کردند که آن ها را قانع کنند که این هم اثبات است و از اثبات ۱۰۰۰ صفحه ای یک قضیه بدتر نیست. ولی هنوز هم دانشمندان در حسرت یک اثبات ساده برای این قضیه هستند.

 اثباتی که روی کاغذ باشد!

 نکته ی دیگر این که این مسئله با کمک نظریه گراف حل شد.

مار سایت

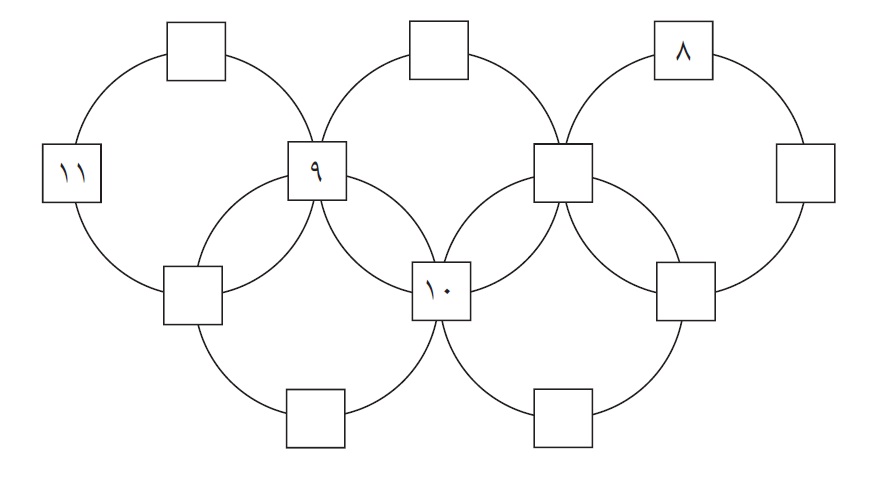
۱- در جای خالی اعداد ۱ تا ۱۲ را طوری قرار دهید که مجموع اعداد روی هر دایره ۲۸ باشد.

۲- در طویله ای چند آدم و چند اسب وجود دارد. اگر آنها در مجموع ۲۲ سر و ۷۲ پا داشته باشند در آنجا چند آدم و چند اسب وجود دارد؟

پاسخ در ((( شما می توانید بالا )))

سوال اینجاست که چه کسی به حضرت محمد (صلوات الله علیه) اینها را آموخته است؟ قرآن هم دقیقاً همین را بیان می‌کند.

آری اگر نگرشمان را به زندگی، گروه و کارمان عوض کنیم زندگی ۱۰۰% خواهد شد.
نگرش همه چیز را عوض می کند، نگاهت را تغییربده چشمهایت را دوباره بشوی همه چیز عوض می شود…

خاطرات دو دوست قدیمی

دو دوست قدیمی در حال عبور از بیابانی بودند. در حین سفر این دو سر موضوع کوچکی بحث میکنند و کار به جایی میرسد که یکی کنترل خشم خودش را از دست میدهد و سیلی محکمی به صورت دیگری میزند. دوست دوم که از شدت ضربه و درد سیلی شوکه شده بود بدون اینکه حرفی بزند روی شنهای بیابان نوشت: "امروز بهترین دوست زندگیم سیلی محکمی به صورتم زد." آنها به راه خود ادامه دادند تا اینکه به دریاچه ای رسیدند. تصمیم گرفتند در آب کمی شنا کنند تا هم از حرارت و گرمای کویر خلاص شوند و هم اتفاق پیش آمده را فراموش کنند.

همچنانکه مشغول شنا بودند ناگهان همان دوستی که سیلی خورده بود حس کرد گرفتار باتلاق شده و گل و لای وی را به سمت پایین میکشد. شروع به داد و فریاد کرد و خلاصه دوستش وی را با هزار زحمت از آن مخمصه نجات داد. مرد که خود را از مرگ حتمی نجات یافته دید، فوری مشغول شد و روی سنگ کنار آب به زحمت حک کرد: "امروز بهترین دوست زندگیم مرا از مرگ قطعی نجات داد." دوستی که او را نجات داده بود وقتی حرارت و تلاش وی را برای حک کردن این مطلب دید با شگفتی پرسید: "وقتی به تو سیلی زدم روی شن نوشتی و حال که تو را نجات دادم روی سنگ حک میکنی؟"

مرد پاسخ داد: "وقتی دوستی تو را آزار میدهد آن را روی شن بنویس تا با وزش نسیم بخشش و عفو آرام و آهسته از قلبت پاک شود. ولی وقتی کسی در حق تو کار خوبی انجام داد، باید آنرا در سنگ حک کنی تا هیچ چیز قادر به محو کردن آن نباشد و همیشه خود را مدیون لطف وی بدانی."

نتیجه اخلاقی : یاد بگیریم آسیبها و رنجشها را در شن بنویسیم تا فراموش شود و خوبی و لطف دیگران را در سنگ حک کنیم تا هیچ گاه فراموش نشود.

مسئله:درافسانه ها می گویند وقتی پادشاه هند ازبازی شطرنج خوشش آمد ، مخترع شطرنج را به حضور طلبید وازاو خواست تا جایزه ای به عنوان پاداش طلب کند . او درخواست خود را این طور مطرح کرد:

"در صفحه شطرنج و در خانه اول ، یک دانه گندم  و در خانه دوم دو برابر خانه اول و در خانه سوم دو برابر خانه دوم گندم قرار دهید . و به همین ترتیب پیش بروید " پادشاه از او درخواست او تعجب کرد و دستور داد به او یک کیسه گندم بدهند . به نظر شما ، آیا درخواست مخترع شطرنج به اندازه ی یک کیسه گندم بوده است .

ابوریحان بیرونی در کتاب "اثار الباقیه عن القرون الخالیه " در حل این مسئله این چنین آورده است :

 18446744703551615

"18 تریلیون و 446 بیلیون و 744 میلیارد و 73 میلیون و 551 هزار و 615 " رسیده  که برای محسوس شدن عدد فوق می گوید :

اگر در سطح کره زمین 2305 کوه را در نظر بگیریم  و از هر کوه 10000 رود جاری شود و در طول رودخانه 1000 قطار شامل قاطر حرکت کند و هر قطار شامل 1000 قاطر باشد و بر هر قاطر 8 کیسه گندم قرار داده باشیم و در هر کیسه 10000 دانه گندم باشد ان وقت این تعداد گندم از تعداد دانه های گندم صفحه شطرنج کوچکتر خواهد شد .

 تعدد دانه های گندم یک تصاعد هندسی را تشکیل می دهند

*برج هانوی*

مسئله برج هانوی به افسانه ای از هندوستان بازمی گردد. در یکی از معابد هندوستان سه ستون وجود داشته که در یکی 64 عدد حلقه به ترتیب قطرشان و جود داشته است. موبدان بر این باور بوده اند که هر گاه توانستند تمام این 64 حلقه را به به ستون سوم ببرند ، عمر جهان پیدا شده و دنیا به پایان خواهد رسید. بتا بر این موبدان دست به کار شدند و شروع به انتقال دادن حلقه ها کردند.

البته در این انتقال :

1- در هر جابجایی تنها یک حلقه را جابجا کنند

2- حلقه بزرگتر روی کوچکتر قرار نگیرد.

تعداد جابجایی ها به ازای n حلقه برابر 2ⁿ -1 جابجایی است . پس موبدان اگر در هر ثانیه یک حلقه را جابجا کنند  باید 2⁶⁴ ثانیه یعنی تقریبا 584 بیلیون سال!!!

سوال: تالار نمایش را به چه شکلی باید ساخت تا تماشاچیانی که در طول ديوار آن نشسته اند از همه جا ، سن نمایش را به یک زاویه ببینند؟

در اين مقاله با نمايش انيميشن هايي ، چند شكل هندسي جديد را به شما معرفي مي كنيم :

الف) دلگون(Cardioid) :اگر دايره اي به شعاع 1 واحد مماس بر دايره اي به شعاع 1 واحد، حول آن بغلتد،شكلي كه يك نقطه از محيط دايره ي غلتان بر آن حركت مي كند را دلگون گويند . 

روزی یکی از دانش آموزان پس از ورود معلم به کلاس از جا برخاست و گفت : اجازه آقا من چند رابطه ي عجیب در ریاضی را ثابت کرده ام .
معلم که شور واشتیاق این دانش آموز را دید از او خواست که پای تابلو بیاید و رابطه هايش را بنویسد .
شاگرد پای تابلو آمدوبا کمال تعجب نوشت :

اولین زن ریاضی دان که در تاریخ ریاضی از او نام برده شده : هیپاتیا

اولین فرد شناخته شده ای که کشفیات ریاضی به او نسبت داده شده : تالس

اولین فردی که یک کتاب منسجم در هندسه منتشر کرد : بقراط خیوسی

اولین کسی که مقاطع مخروطی را ارائه کرد : منایخموس

اولین کسی که تلاش جدی در فلسفه ی ریاضی به عمل آورد : افلاطون

اولین ارائه دهنده ی نظریه ی اتمی بودن جهان : دموکریتوس

اولین کسی که در مسئله ی تضعیف مکعب به پیشرفت دست یافت : بقراط خیوسی

اولین ارائه دهنده ی برهان برای حل مسئله ی تثلیث زاویه به کمک مقاطع مخروطی : پاپوس

اولین فرد یونانی که ارتباطش با مسئله ی تربیع معلوم است : آناکساگوراس

اولین چاپ اصول اقلیدس : سال 1482

اولین فردی که ترجمه ی انگلیسی کاملی از اصول اقلیدس ارائه داد : بیلینگزلی

اولین کسی که کوشش کرد اصول ریاضی را تدوین کند : بقراط

اولین کسی که معادلات درجه دوم را به روش هندسی حل کرد : دیوفانتوس

اولین کسی که ترجمه ی عربی واقعا رضایت بخش از اصول اقلیدس ارائه کرد : ثابت ابن قره

اولین کسی که کتابی در حساب به زبان عربی تالیف کرد : خوارزمی

اولین نویسنده ی عربی نویس که با قضیه ی دو جمله ای در شکل مثلث پاسکال کار کرد : کاشانی

اولین نمونه ی کار ریاضی اصیل که توسط اعراب انجام شده : قائده ی ثابت ابن قره برای یافتن اعداد متحابه

اولین شرح منسجم از مثلثات مسطحه و کروی در اروپا که مستقل از نجوم مورد مطاعه قرار می گرفت :

تریانگولیس اومنیودیس اثر یوهان مولر

اولین کسی که علامت های + و – را به کار برد : یوهان ویدمان

یک من = 3 کیلو

ری = 4 من

خروار = 100 من

چارک = یک چهارم من

سیر = یک دهم چارک = یک چهلم من

مثقال = یک شانزدهم سیر

قیراط = یک بیست و سوم مثقال

نخود = یک بیست و چهارم مثقال

گندم = یک چهارم نخود


واحد های اندازه گیری طول در ایران قدیم

یک ذرع = 104 سانتیمتر

چارک = یک چهارم ذرع

گره = یک چهازم چارک = یک شانزدهم ذرع

بهر = یک دوم گره = یک هشتم چارک = یک سی و دوم ذرع

فرسخ = 6000 ذرع

البته بعضی واحدها در برخی از مناطق کشور تفاوت دارد

Character and Excellence

Sunflowers and Pinecones - The individual florets of the sunflower (and of the daisy as well) grow in two spirals extending out from the center in opposite directions. The first spiral has 21 arms, while the other has 34. These are Fibonacci numbers, and have the Golden Ratio. Similarly, pinecones have 5 and 8 arms, or 8 and 13 arms depending on their size. This arrangement has been identified as the most efficient way of filling the space on the pinecone with seeds.

Daisies - Most daisies have 21, 34, 55, or 89 petals - all Fibonacci numbers.

Spiral Growth - The Golden Angle, also derived from the Golden Ratio, approximates to 137.51°. This is often the angle found between successive florets or leaves, in spiral growth.

بـه سلامتـی تـو ...

(جملات زیبا و پرمعنی)



به سلامتی رفیقی که تو رفاقت کم نذاشت ولی کم برداشت تا رفیقش کم نیاره ...
.
.
.
به سلامتی مداد پاک کن که به خاطر اشتباه دیگران خودشو کوچیک میکنه ...
.
.
.
به سلامتی اون دلی که هزار بار شکست ولی هنوزم شکستن بلد نیست ...
.
.
.
به سلامتی اونایی که تو اوج سختی ها و مشکلات به جای اینکه تَرکمون کنن درکمون می کنن ...
.
.
.
به سلامتی اونایی که درد دل همه رو گوش میدن اما معلوم نیس خودشون کجا درد دل میکنن ...
.
.
.
به سلامتی اونی که باخت تا رفیقش برنده باشه ...
.
.
.
به سلامتی کسی که هنوز دوسش داری ولی دیگه مال تو نیست ...
.
.
.
به سلامتی مادر که وقتی غذا سر سفره کم بیاد اولین کسی که از اون غذا دوس نداره خودشه ...
.
.
.
به سلامتی همه اونایی که خطشون اعتباریه ولی معرفتشون دائمیه!
.
.
.
به سلامتی اونایی که به پدر و مادرشون احترام میذارن و میدونن تو خونه ای که بزرگترها کوچک شوند؛ کوچکترها هرگز بزرگ نمیشوند ...
.
.
.
به سلامتی مادر که بخاطر ما هیکلش به هم خورد !
.
.
.
به سلامتی کسی که دید بغلیش تو تاکسی پول نداره
به راننده گفت : پول خورد ندارم مال همه رو حساب کن!
.
.
.
به سلامتی بیل! که هرچ‌قدر بره تو خاک، بازم برّاق‌تر می‌شه ...
.
.
.
به سلامتی سیم خاردار! که پشت و رو نداره ...
.
.
.
به سلامتی اونی که بیکسه، ولی ناکس نیست ...
.
.
.
به سلامتی اونایی که چه عشقشون پیششون باشه چه نباشه چشمشون مثل فانوس دریایی نمی چرخه ...
.
.
.
به سلامتی حلقه های زنجیر که زیر برف و بارون میمونن زنگ میزنن ولی هم دیگه رو ول نمیکنن ...
.
.
.
گل آفتابگردان را گفتند:
چرا شبها سرت را پایین می اندازی؟
گفت : ستاره چشمک میزند، نمیخواهم به خورشید خیانت کنم
به سلامتی همه اونایی که مثل گل آفتابگردان هستند ...
.
.
.
بسلامتی اون دختری که حاضره زیر بارون خیس بشه ولی‌ سوار ماشین هیچ پسری نشه ...
.
.
.
به سلامتی کسی که وقتی بردم گفت :
اون رفیق منه
وقتی باختم گفت :
من رفیقتم ...
.
.
.
به سلامتی کسی که وقتی بهش زنگ میزنی و خوابه
ولی واسه اینکه دلت رو نشکنه میگه: خوب شد زنگ زدی؛ باید بیدار میشدم ...
.
.
.
به سلامتی‌ اون بچه‌ای که شیمی‌ درمانی کرده همه ی موهاش ریخته
به باباش میگه بابا من الان شدم مثل رونالدو یا روبرتو کارلوس؟
باباش میگه قربونت برم از همه اونا تو خوش تیپ تری ...
.
.
.
به سلامتی‌ اون پسری که وقتی‌ تو خیابون نگاهش به یه دختر ناز و خوشگل میفته
بازم سرشو میندازه پایین و زیر لب میگه: اگه آخرشم باشی‌
انگشت کوچیکهٔ عشقم هم نیستی ...
.
.
.
به سلامتی دریا که همه با لبش خاطره دارن !
.
.
.
به سلامتی همه اوونایی که
دلشون از یکی دیگه گرفته
ولی برای اینکه خودشون رو آروم کنن
میگن بخاطر غروب پاییزه ...
.
.
.
بسلامتی با ارزش ترین پول دنیا "تومن"
چون هم تو هستی توش، هم من ...
.
.
.
به سلامتی اونایی که اگه صد لایه ایزوگامشون هم بکنن بازم معرفت ازشون چیکه میکنه ...
.
.
.
به سلامتی اونایی که دوسشون داریم و نمیفهمن !
آخرشم دق میدن مارو !
.
.
.
سلامتی همه کلاس اولی ها که تازه امسال یاد میگیرن سلامتی درسته نه صلامتی!
.
.
.
به سلامتی اون پسری که خواست آدم بشه ...
ولی یه دختر اومد تو زندگیش و نذاشت و بهش فهموند که
همیشه پای یک زن در میان است !
.
.
.
به سلامتی پسر بچه های قدیم که پشت لبشونو با ذغال سیاه می کردن
که شبیه باباهاشون بشن
نه مثل جوونای امروز که ابروهاشونو نازک می کنن که شبیه ماماناشون بشن !
.
.
.
به سلامتی کسیکه تو خیالمونه ولی بیخیالمونه ...
.
.
.
به سلامتی دوست خوبی که
مثل خط سفید وسط جاده است
تکه تکه میشه
ولی بازم پا به پات میاد ...
.
.
.
به سلامتی باغچه ای که خاکش منم گلش تویی و خارش هرچی نامرده ...
.
.
.
به سلامتی پدری که لباس خاکی و کثیف میپوشه
میره کارگری برای سیر کردن شکم بچه اش،
اما بچه اش خجالت میکشه
به دوستاش بگه که این پدرمه ...
.
.
.
به سلامتی نوشابه که خانواده داره و خیلی ها همینش هم ندارن !
.
.
.
به سلامتی سندباد که کل دنیا رو با یه شلوار کردی دور زد ...
.
.
.
به سلامتی سرنوشت که نمی‌شه اونو از سر نوشت ...
.
.
.
به سلامتی اون رفتگری که تو این هوای سرد و وانفسای بی عدالتی داره به عشق زن و بچه اش کوچه و خیابون رو جارو میزنه که یه لقمه نون حلال در بیاره ...
.
.
.
به سلامتی اون کارگری که از افتضاح اختلاس 3000 میلیارد تومانی خبر داره اما باز اول صبح بچه شو میبوسه و برای ماهی 200 هزار تومان پول حلال میره سر کار و عرق میریزه ...
.
.
.
به سلامتی اونهائی که دوستت دارم رو درک می کنند و اونو به حساب کمبودهات نمی ذارن ...
.
.
.
به سلامتی همه ی اونایی که مارو همین جوری که هستیم دوست دارن ...
.
.
.
به سلامتی دوست نازنینی که گفت: قبر منو خیلی بزرگ بسازین... چون دارم یه دنیا آرزو با خودم به گور میبرم !
.
.
.
و در آخر به سلامتی تو، که از همه بهترینی ...

هنرمندی به نام جانت اچلمان با جدی گرفتن تخیلش این آثار را خلق کرده است. این هنرمند با استفاده از تور و رنگ، طراحی های بسیار زیبایی را برای مکان های مختلف خلق کرده که در شب با تابش نور زیبابی های آن دو چندان می شود.

..

..

..

سخنـان نــاب و پرمعنــای زنـدگی



در روزگاری که خنده ی مردم از زمین خوردن توست،
پس برخیز تا چنین مردمی بگریند ...
.
.
.
درصد کمی از انسانها نود سال زندگی می کنند
مابقی یک سال را نود بار تکرار می کنند
.
.
.
نصف اشباهاتمان ناشی از این است که
وقتی باید فکر کنیم، احساس می کنیم
و وقتی که باید احساس کنیم، فکر می کنیم
.
.
.
سر آخر، چیزی که به حساب می آید تعداد سالهای زندگی شما نیست
بلکه زندگی ای است که در آن سالها کرده اید
.
.
.

کلمات انگلیسی با تعبیر فارسی! (طنز)



Keyboard
چه کسی برنده شد؟

Communication Board
کامیون کی شن ها رو برد؟

Morphine
باید بیشتر فین کنی

MissCall
دختر نا بالغ را گویند

Freezer
حرف مفت

Suspicious
به لهجه اصفهانی: ساس از بقیه ی حشرات جلو تر است

Johnny Depp
قاتل افسرده

Acer
ای آقا!

Welcome
دهن لق

Manual
من و بقیه

Accessible
عکس سیبیل

بــازی روزگـــار
از دلنوشته های پروفسور حسابی (پدر فیزیك ایران)


بازی روزگار را نمی فهمم!
من تو را دوست می دارم... تو دیگری را... دیگری مرا... و همه ما تنهاییم!

داستان غم انگیز زندگی این نیست که انسانها فنا می شوند،
این است که آنان از دوست داشتن باز می مانند.

همیشه هر چیزی را که دوست داریم به دست نمی آوریم،
پس بیاییم آنچه را که به دست می آوریم دوست بداریم.

انسان عاشق زیبایی نمی شود،
بلكه آنچه عاشقش می شود در نظرش زیباست!

انسان های بزرگ دو دل دارند؛
دلی که درد می کشد و پنهان است و دلی که میخندد و آشکار است.

همه دوست دارند که به بهشت بروند،
ولی کسی دوست ندارد که بمیرد ... !

عشق مانند نواختن پیانو است،
ابتدا باید نواختن را بر اساس قواعد یاد بگیری. سپس قواعد را فراموش کنی و با قلبت بنوازی.

دنیا آنقدر وسیع هست که برای همه مخلوقات جایی باشد،
پس به جای آنکه جای کسی را بگیریم تلاش کنیم جای واقعی خود را بیابیم.

‏‏اگر انسانها بدانند فرصت باهم بودنشان چقدر محدود است؛
محبتشان نسبت به یکدیگر نامحدود می شود.

عشق در لحظه پدید می آید
و دوست داشتن در امتداد زمان
و این اساسی ترین تفاوت میان عشق و دوست داشتن است.راه دوست داشتن هر چیز درک این واقعیت است که امکان دارد از دست برود :

انسان چیست ؟
شنبه: به دنیا می آید.
یكشنبه: راه می رود.
دوشنبه: عاشق می شود.
سه شنبه: شكست می خورد.
چهارشنبه: ازدواج می كند.
پنج شنبه: به بستر بیماری می افتد.
جمعه: می میرد.
فرصت های زندگی را دریابیم و بدانیم که فرصت با هم بودن چقدر محدود است ...